Non-Hermitian dynamics |
|
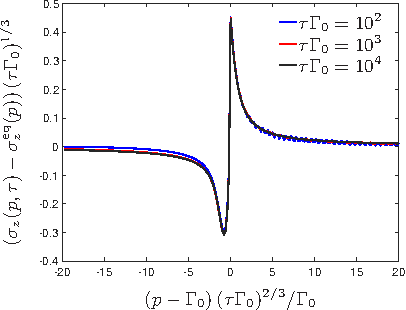 |
Upon driving a quantum system through a critical point, defects are produced, whose density obeys a scaling form in terms of the equilibrium critical exponents. This is accounted for by the Kibble-Zurek theory and plays a crucial role in quantum and statistical mechanics, cosmology and condensed matter physics. Parallel to these developments, there is a recent surge of interest in understanding and analyzing non-hermitian Hamiltonians. At an exceptional point, which is the generalization of a critical point to the non-hermitian realm, several complex eigenvalues and eigenstates coalesce. The ensuing dynamics is thus expected to be completely distinct from what we are used to in hermitian quantum mechanics. We investigate the Kibble-Zurek theory for various exceptional points and protocols and determine its universal scaling form in non-hermitian systems
Reference: B. Dóra, M. Heyl, R. Moessner, Nature Communication 10, 2254 (2019) |
Strongly correlated quantum systems |
|
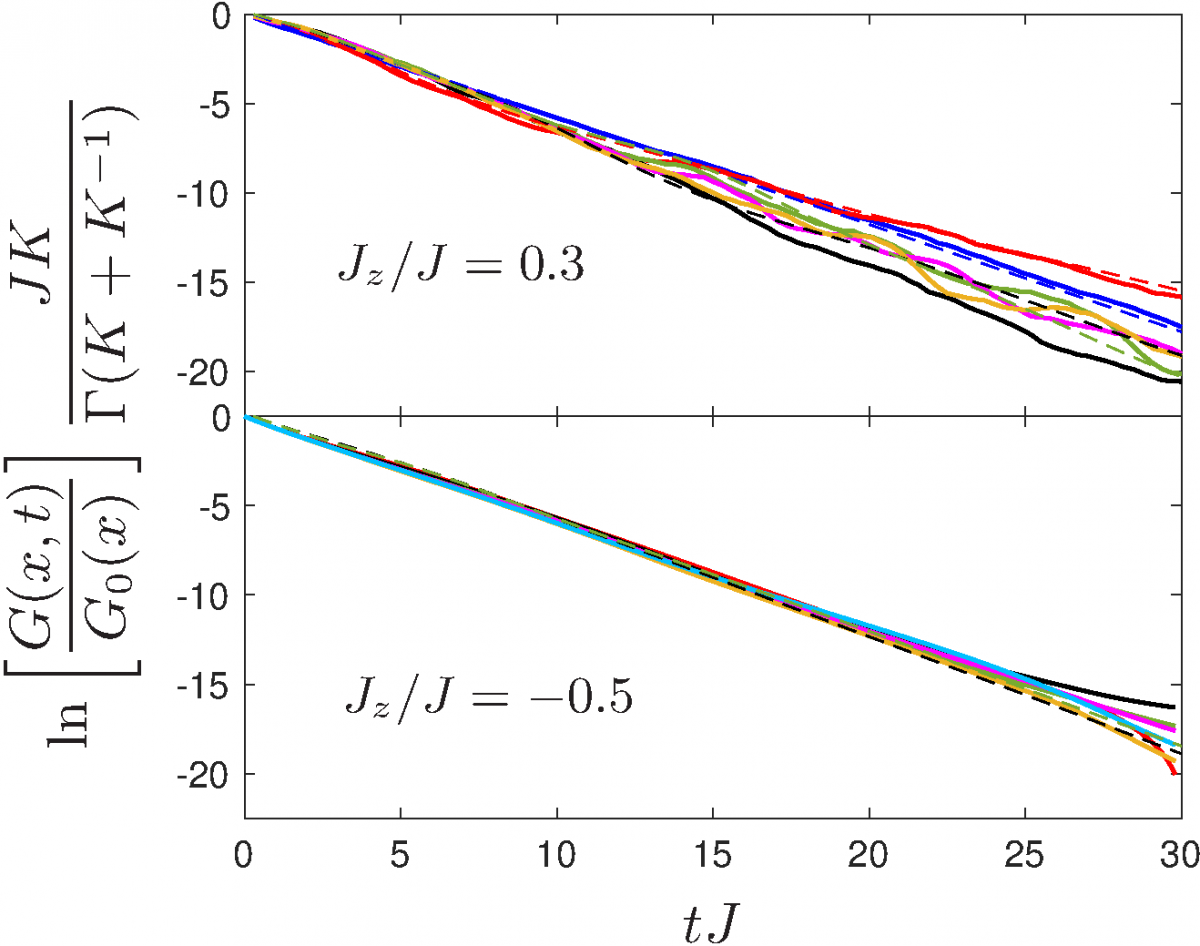 |
Luttinger liquids are ubiquitous in one dimension and display universal physics in and out of equilubrium in closed quantum systems. We focus on their response upon suddenly coupling it to a dissipative environment. The single particle density matrix Reference: Á. Bácsi, P. Moca, G. Zaránd, B. Dóra, Physical Review Letters 124, 266803 (2020)
|
Dynamical quantum phase transitions |
|
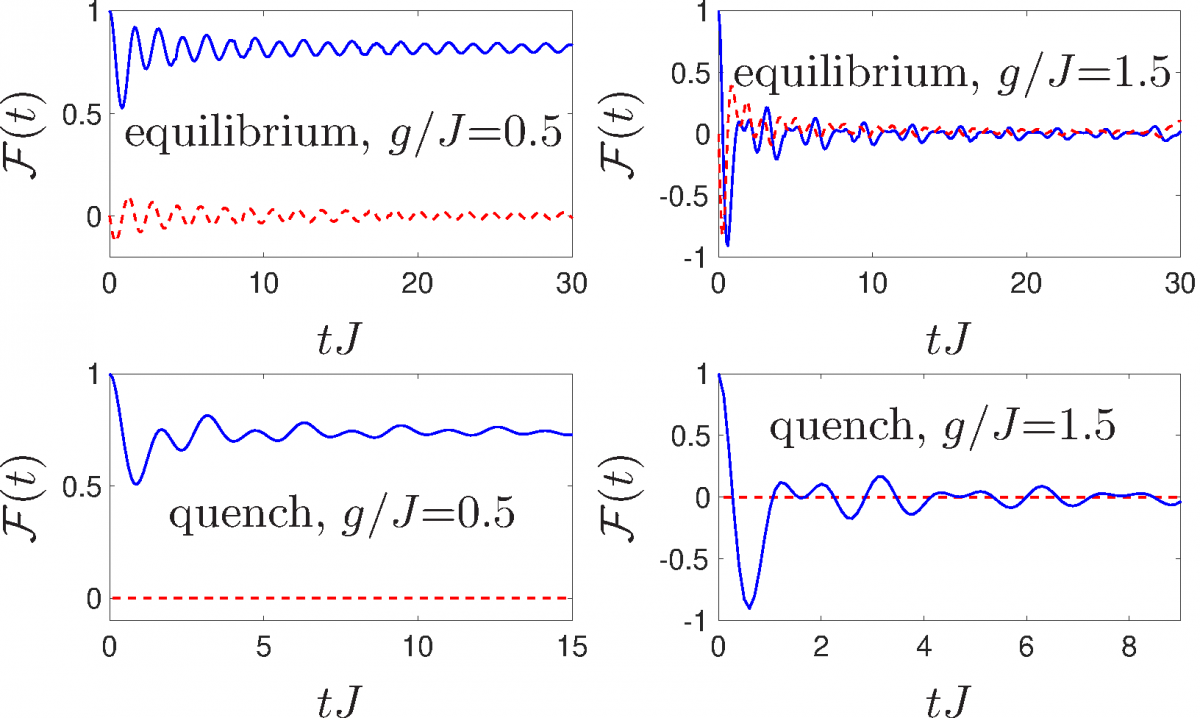 |
Out-of-time-ordered (OTO) correlators have developed into a central concept quantifying quantum information transport, information scrambling and quantum chaos. The OTO correlator can also be used to dynamically detect equilibrium as well as nonequilibrium phase transitions in Ising chains. We study OTO correlators of an order parameter both in equilibrium and after a quantum quench for different variants of transverse-field Ising models in one dimension, including the integrable one as well as non-integrable and long-range extensions. For all the studied models that the OTO correlator in ground states detects the quantum phase transition.After a quantum quench from a fully polarized state we observe numerically for the short-range models that the asymptotic long-time value of the OTO correlator signals still the equilibrium critical points and ordered phases. For the long-range extension, the OTO correlator instead determines a dynamical quantum phase transition in the model. Reference: M. Heyl, F. Pollmann, B. Dóra: Physical Review Letters 121 016801 (2018)
|

